JEE Advanced Previous Year Questions of Math with Solutions are available at eSaral. Practicing JEE Advanced Previous Year Papers Questions of mathematics will help the JEE aspirants in realizing the question pattern as well as help in analyzing weak & strong areas.
eSaral helps the students in clearing and understanding each topic in a better way. eSaral also provides complete chapter-wise notes of Class 11th and 12th both for all subjects.
Besides this, eSaral also offers NCERT Solutions, Previous year questions for JEE Main and Advance, Practice questions, Test Series for JEE Main, JEE Advanced and NEET, Important questions of Physics, Chemistry, Math, and Biology and many more.
Download eSaral app for free study material and video tutorials.
Q. The number of values of $\theta$ in the interval $\left(\frac{-\pi}{2}, \frac{\pi}{2}\right)$ such that $\theta \neq \frac{n \pi}{5}$ for $n=0, \pm 1, \pm 2$ and $\tan \theta=\cot 5 \theta$ as well as $\sin 2 \theta=\cos 4 \theta,$ is
[JEE 2010, 3]
Ans. 3
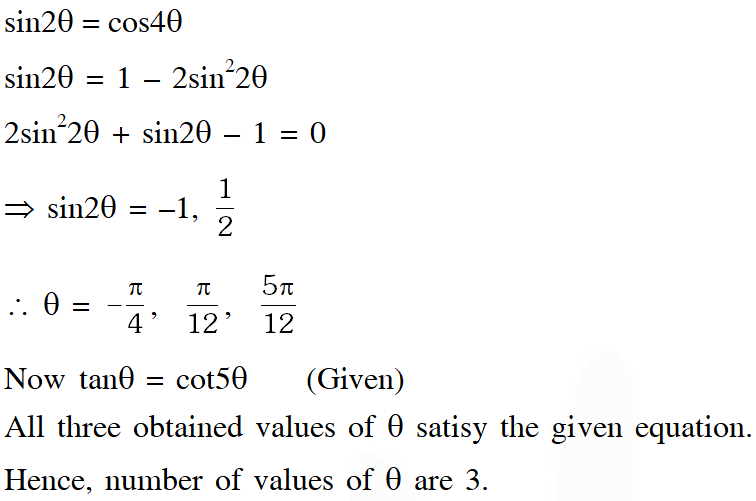
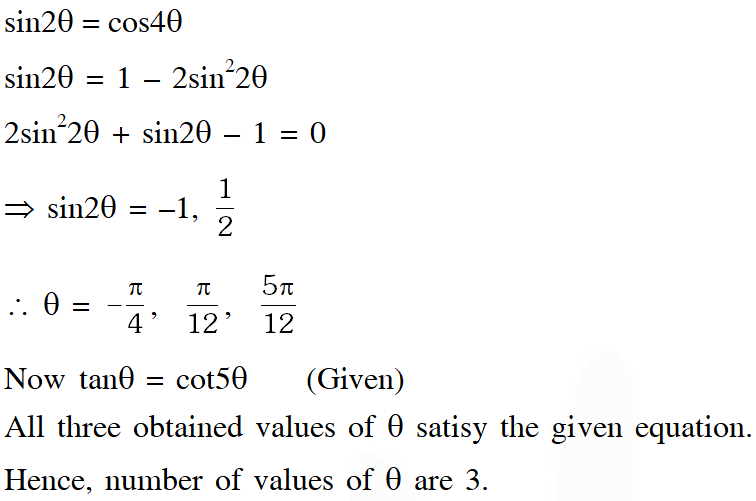
Q. The positive integer value of n > 3 satisfying the equation
$\frac{1}{\sin \left(\frac{\pi}{\mathrm{n}}\right)}=\frac{1}{\sin \left(\frac{2 \pi}{\mathrm{n}}\right)}+\frac{1}{\sin \left(\frac{3 \pi}{\mathrm{n}}\right)}$ is
[JEE 2011, 4]
Ans. 7
$\frac{1}{\sin \frac{\pi}{\mathrm{n}}}=\frac{1}{\sin \frac{2 \pi}{\mathrm{n}}}+\frac{1}{\sin \frac{3 \pi}{\mathrm{n}}}$
$\Rightarrow \frac{1}{\sin \frac{\pi}{\mathrm{n}}}-\frac{1}{\sin \frac{3 \pi}{\mathrm{n}}}=\frac{1}{\sin \frac{2 \pi}{\mathrm{n}}}$
$\Rightarrow \frac{\sin \frac{3 \pi}{n}-\sin \frac{\pi}{n}}{\sin \frac{\pi}{n} \sin \frac{3 \pi}{n}}=\frac{1}{\sin \frac{2 \pi}{n}}$
$\Rightarrow \frac{2 \cos \frac{2 \pi}{\mathrm{n}} \sin \frac{\pi}{\mathrm{n}}}{\sin \frac{\pi}{\mathrm{n}} \sin \frac{3 \pi}{\mathrm{n}}}=\frac{1}{\sin \frac{2 \pi}{\mathrm{n}}}$
$\Rightarrow 2 \cos \frac{2 \pi}{\mathrm{n}} \sin \frac{2 \pi}{\mathrm{n}}=\sin \frac{3 \pi}{\mathrm{n}}$
$\Rightarrow \sin \frac{4 \pi}{\mathrm{n}}=\sin \frac{3 \pi}{\mathrm{n}} \Rightarrow \frac{4 \pi}{\mathrm{n}}=\mathrm{K} \pi+(-1)^{\mathrm{K}} \frac{3 \pi}{\mathrm{n}}$
If $\mathrm{K}=2 \mathrm{m} \quad \Rightarrow \quad \frac{\pi}{\mathrm{n}}=2 \mathrm{m} \pi$
$\Rightarrow \quad n=\frac{1}{2 m} \quad \Rightarrow n=\frac{1}{2}, \frac{1}{4}, \frac{1}{6} \ldots \ldots$
If $\mathrm{K}=2 \mathrm{m}+1 \Rightarrow \frac{7 \pi}{\mathrm{n}}=(2 \mathrm{m}+1) \pi$
$\Rightarrow \mathrm{n}=\frac{7}{2 \mathrm{m}+1} \quad \Rightarrow \quad \mathrm{n}=7, \frac{7}{3}, \frac{7}{5} \ldots \ldots$
Possible value of n is 7
Q. Let $\theta, \varphi \in[0,2 \pi]$ be such that $2 \cos \theta(1-\sin \varphi)=\sin ^{2} \theta\left(\tan \frac{\theta}{2}+\cot \frac{\theta}{2}\right) \cos \varphi-1, \tan (2 \pi-\theta)>0$
and $-1<\sin \theta<-\frac{\sqrt{3}}{2} .$ Then $\varphi$ cannot satisfy-
(A) $0<\varphi<\frac{\pi}{2}$
(B) $\frac{\pi}{2}<\varphi<\frac{4 \pi}{3}$
(C) $\frac{4 \pi}{3}<\varphi<\frac{3 \pi}{2}$
(D) $\frac{3 \pi}{2}<\varphi<2 \pi$
[JEE 2012, 4M]
Ans. (A,C,D)


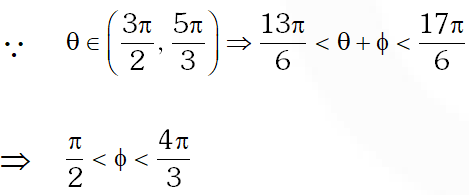


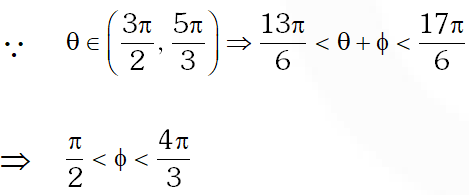
Q. For $\mathrm{x} \in(0, \pi),$ the equation $\sin \mathrm{x}+2 \sin 2 \mathrm{x}-\sin 3 \mathrm{x}=3 \mathrm{has}$
(A) infinitely many solutions
(B) three solutions
(C) one solution
(D) no solution
[JEE(Advanced)-2014, 3(–1)]
Ans. (D)
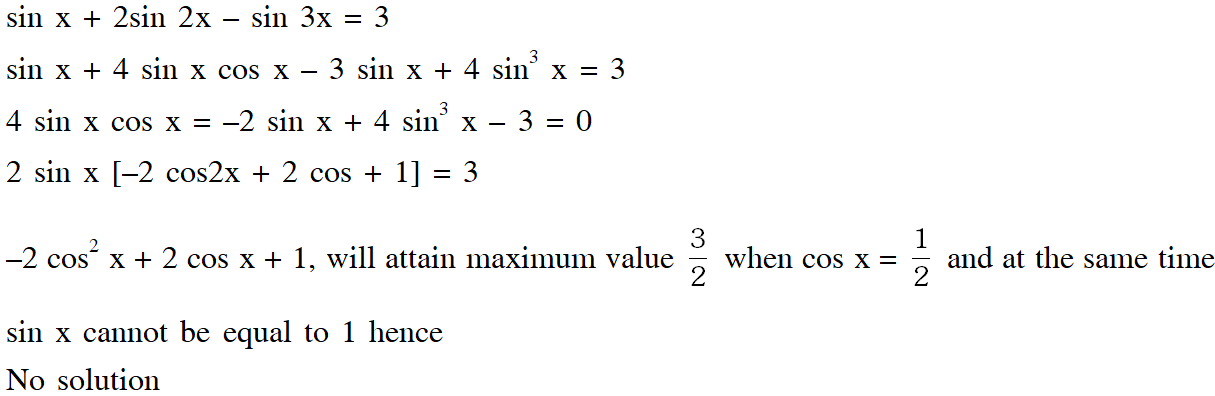
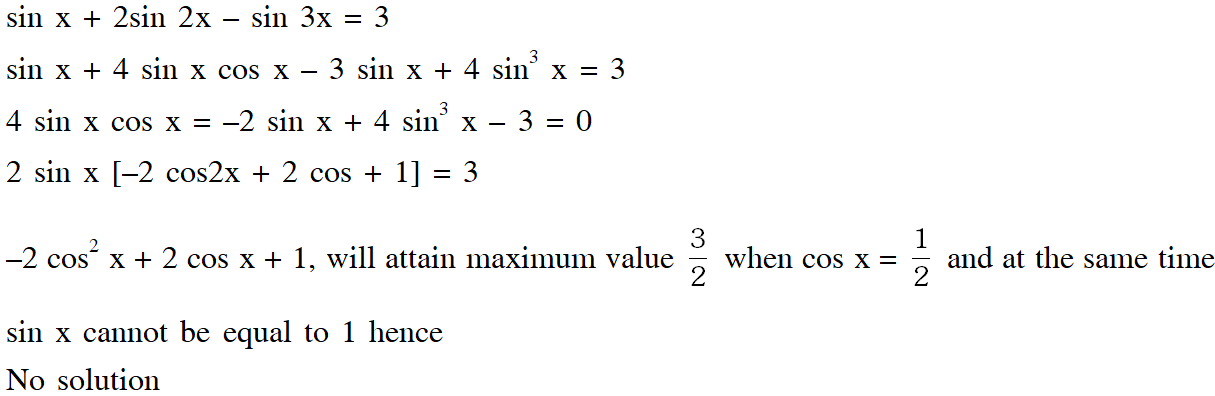
Q. The number of distinct solutions of equation $\frac{5}{4} \cos ^{2} 2 x+\cos ^{4} x+\sin ^{4} x+\cos ^{6} x+\sin ^{6} x=2$ in the interval $[0,2 \pi]$ is
[JEE 2015, 4M, –0M]
Ans. 8
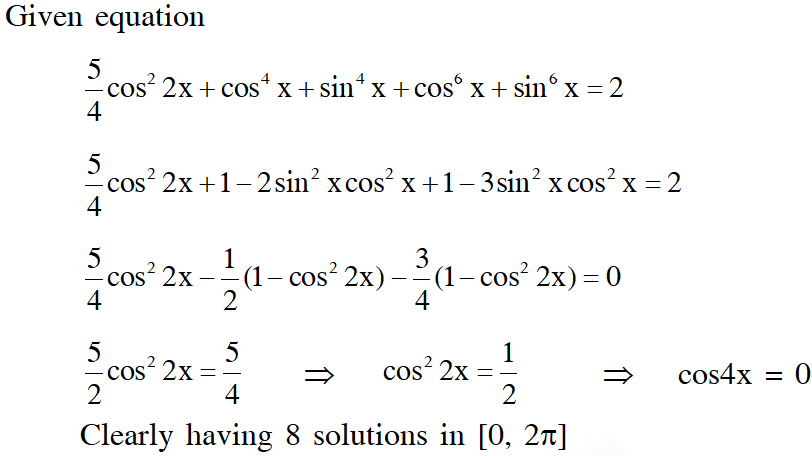
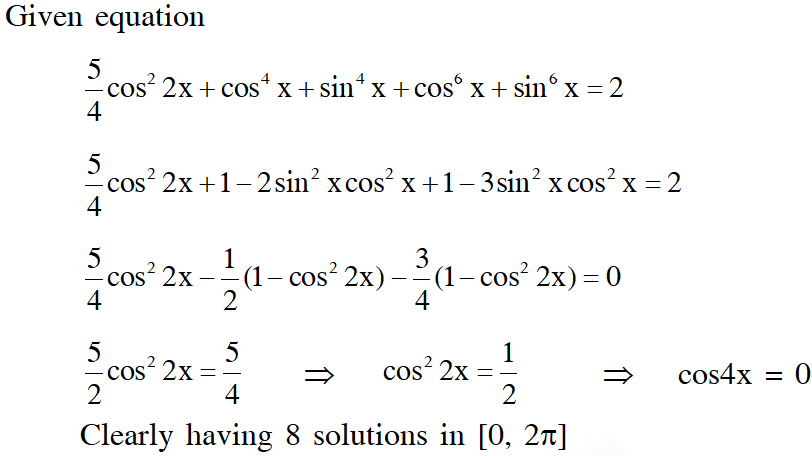
Q. Let $S=\left\{x \in(-\pi, \pi): x \neq 0, \pm \frac{\pi}{2}\right\} .$ The sum of all distinct solution of the equation $\sqrt{3} \sec x+\csc x+2(\tan x-\cot x)=0$ in the set $S$ is equal to $-$
(A) $-\frac{7 \pi}{9}$
(B) $-\frac{2 \pi}{9}$
(C) 0
(D) $\frac{5 \pi}{9}$
[JEE(Advanced)-2016]
Ans. (C)
$\sqrt{3} \sin x+\cos x=2 \cos 2 x$
$\Rightarrow \cos 2 x=\cos \left(x-\frac{\pi}{3}\right)$
$\Rightarrow 2 x=2 n \pi \pm\left(x-\frac{\pi}{3}\right)$
$\quad \quad x=(6 n-1) \frac{\pi}{3}$ or $(6 n+1) \frac{\pi}{9}$
$\Rightarrow x=-\frac{\pi}{3}, \frac{\pi}{9}, \frac{7 \pi}{9}$ and $-\frac{5 \pi}{9}$ in $(-\pi, \pi)$
$\Rightarrow \operatorname{sum}=0$
Q. Let $a, b, c$ be three non-zero real numbers such that the equation $\sqrt{3} a \cos x+2 b \sin x=c, \quad x$ $\in\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]$ has two distinct real roots $\alpha$ and $\beta$ with $\alpha+\beta=\frac{\pi}{3} .$ Then the value of $\frac{b}{a}$ is $-$
$=$
[JEE(Advanced)-2018]
Ans. 0.5

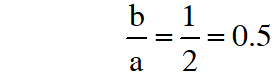

Comments
Shibi bessanio
Feb. 18, 2021, 8:39 p.m.
Nice question but those can be solved by further methods so not harder
