Yash scored 40 marks in a test, getting 3 marks for each right answer and losing 1 mark for each wrong answer.

Let take right answer will be $x$ and wrong answer will be $y$.

Hence total number of questions will be $x+y \cdots(i)$

If yash scored 40 marks in atleast getting 3 marks for each right answer and losing 1 mark for each wrong answer then

$3 x-1 y=40 \cdots(i i)$

If 4 marks awarded for each right answer and 2 marks deduced for each wrong answer the he scored 50 marks

$4 x-2 y=50 \cdots($ iii $)$

By multiplying equation $(i)$ by 2 we get

$6 x-2 y=80 \cdots(i v)$

By subtracting $(i i i)$ from $(i v)$ we get

$x=\frac{30}{2}$

$x=15$

Putting $x=15$ in equation $(i i)$ we have

$3 x-1 y=40$

$3 \times 15-1 y=40$

$45-1 y=40$

$-1 y=40-45$

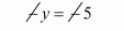
Total number question will be

$=x+y$

$=15+5$

$=20$

Hence, the total number of question is 20.