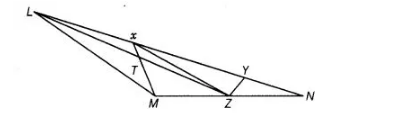
$X$ and $Y$ are points on the side $L N$ of the triangle $L M N$ such that $L X=X Y=Y N$. Through $X$, a line is drawn parallel to $L M$ to meet $M
N$ at $Z$ (see figure). Prove that ar $(\Delta L Z Y)=\operatorname{ar}(M Z Y X)$.
Thinking Process
Use the property that the triangles on the same base and between the same two parallel lines are equal in area. Further prove the required result.
Given X and Y are points on the side LN such that
LX = XY = YN and XZ || LM To prove ar (ΔLZY) = ar (MZYX)
Proof Since, ΔXMZ and ΔXLZ are on the same base XZ and between the same parallel lines LM and XZ.
Then, ar (ΔXMZ) = ar (ΔXLZ) …(i)
On adding ar (ΔXYZ) both sides of Eq. (i), we get
ar (ΔXMZ) + ar (ΔXXZ) = ar (ΔXLZ) + ar (ΔXYZ)
=> ar (MZYX) = ar (ΔLZY) Hence proved.
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.