Write the set of values of a and b for which the following system of equations has infinitely many solutions.

Solution:

The given equations are

$2 x+3 y-7=0$

$2 a x+(a+b) y-28=0$

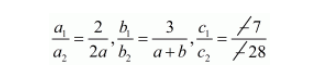
For the equations to have infinite number of solutions,

$\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}$

Therefore

$\frac{2}{2 a}=\frac{3}{a+b}=\frac{7}{28}$

Let us take

$\frac{2}{2 a}=\frac{3}{a+b}$

$2(a+b)=2 a \times 3$

$2 a+2 b=6 a$

$0=6 a-2 a-2 b$

$0=4 a-2 b$

$\frac{3}{a+b}=\frac{7}{28}$

$28 \times 3=7(a+b)$

$84=7 a+7 b$

By dividing both the sides by 7 we get,

$12=a+b \cdots(i i)$

By multiplying equations $($ ii $)$ by 2 we get

$24=2 a+2 b \cdots(i i i)$

Substituting $(i i i)$ from $(i)$ we get

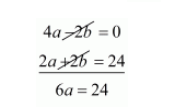
$a=\frac{24}{6}$

$a=4$

Subtracting $a=4$ in equation (iii) we have

$24=2 a+2 b$

$24=2 \times 4+2 b$

 

$24=8+2 b$

$24-8=2 b$

$16=2 b$

$\frac{16}{2}=b$

$8=b$

Hence, the value of $a=4, b=8$ when system of equations has infinity many solutions.