Write the correct alternative in the following:
If $y=a \cos \left(\log _{e} x\right)+b \sin \left(\log _{e} x\right)$, then $x^{2} y_{2}+x y_{1}=$
A. 0
B. $y$
C. $-y$
D. none of these
Given:
$y=a \cos \left(\log _{e} x\right)+b \sin \left(\log _{e} x\right)$
$\frac{d y}{d x}=-a \sin \left(\log _{e} x\right) \frac{1}{x}+b \cos \left(\log _{e} x\right) \frac{1}{x}$
$x y_{1}=-a \sin \left(\log _{e} x\right)+b \cos \left(\log _{e} x\right)$
$\frac{d^{2} y}{d x^{2}}=-a \cos \left(\log _{e} x\right) \frac{1}{x^{2}}+\frac{1}{x^{2}} a \sin \left(\log _{e} x\right)-b \sin \left(\log _{e} x\right) \frac{1}{x^{2}}+b \cos \left(\log _{e} x\right) \frac{1}{x^{2}}$
$x^{2} y_{2}=-a \cos \left(\log _{e} x\right)+a \sin \left(\log _{e} x\right)-b \sin \left(\log _{e} x\right)-b \cos \left(\log _{e} x\right)$
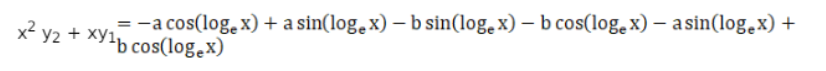
$=-a \sin \left(\log _{e} x\right)-b \cos \left(\log _{e} x\right)$
$=-y$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.