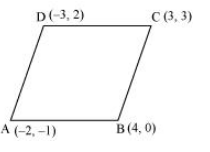
Without using distance formula,

Let points (–2, –1), (4, 0), (3, 3), and (–3, 2) be respectively denoted by A, B, C, and D.

Slope of $A B=\frac{0+1}{4+2}=\frac{1}{6}$

Slope of $C D=\frac{2-3}{-3-3}=\frac{-1}{-6}=\frac{1}{6}$

$\Rightarrow$ Slope of $A B=$ Slope of $C D$

$\Rightarrow \mathrm{AB}$ and $\mathrm{CD}$ are parallel to each other.

Now, slope of $B C=\frac{3-0}{3-4}=\frac{3}{-1}=-3$

Slope of $A D=\frac{2+1}{-3+2}=\frac{3}{-1}=-3$

$\Rightarrow$ Slope of $B C=$ Slope of $A D$

$\Rightarrow \mathrm{BC}$ and $\mathrm{AD}$ are parallel to each other.

Therefore, both pairs of opposite sides of quadrilateral ABCD are parallel. Hence, ABCD is a parallelogram.

Thus, points (–2, –1), (4, 0), (3, 3), and (–3, 2) are the vertices of a parallelogram.