With the vertices A, B and C of a triangle ABC as centres, arcs are drawn with radii 5 cm each as shown in the given figure.

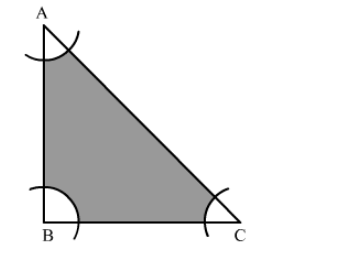
Given that ABC is a triangle with sides AB = 14 cm, BC = 48 cm, CA = 50 cm.
Clearly it is a right angled triangle.

Area of $\triangle \mathrm{ABC}=\frac{1}{2} \times$ base $\times$ height $=\frac{1}{2} \times 48 \times 14=336 \mathrm{~cm}^{2}$

Now we need to remove the area of 3 arcs each of radius 5 cm from this area of triangle.

Here, $\angle \mathrm{B}=90^{\circ}, \angle \mathrm{A}+\angle \mathrm{C}=90^{\circ}$

The area of these 3 arcs would exactly be equal to a sector of circle with radius $5 \mathrm{~cm}$ and angle $=\angle \mathrm{A}+\angle \mathrm{B}+\angle \mathrm{C}=180^{\circ}$ i.e. a semi circle.

Since we know that area of semi circle is $\frac{1}{2} \pi r^{2}=\frac{1}{2} \times 3.14 \times 5 \times 5=\frac{1}{2} \times \frac{314}{100} \times 25=\frac{314}{8}=\frac{157}{4} \mathrm{~cm}^{2}$.

Hence, the area of shaded region is $=$ area of $\triangle \mathrm{ABC}-$ combined area of $3 \operatorname{arcs}=336-\frac{157}{4}$

$=336-39.25=296.75 \mathrm{~cm}^{2}$