While covering a distance of 30 km. Ajeet takes 2 hours more than Amit.

Let the speed of Ajeet and Amit be x Km/hr respectively. Then,

Time taken by Ajeet to cover $30 \mathrm{Km}=\frac{30}{x} \mathrm{hrs}$

Time taken by Amit to cover $30 \mathrm{Km}=\frac{30}{y} \mathrm{hrs}$

By the given conditions, we have

$\frac{30}{x}-\frac{30}{y}=2 \cdots(i)$

If Ajeet doubles his speed, then speed of Ajeet is $2 x \mathrm{Km} / \mathrm{hr}$

Time taken by Ajeet to cover $30 \mathrm{Km}=\frac{30}{2 x} \mathrm{hrs}$

Time taken by Amit to cover $30 \mathrm{Km}=\frac{30}{y} \mathrm{hrs}$

According to the given condition, we have

$-15 x+\frac{30}{y}=1$..(ii)

Putting $\frac{1}{x}=u$ and $\frac{1}{y}=v$, in equation (i) and (ii), we get

$30 u-30 v=2 \cdots(i i i)$

$-15 u+30 v=1 \cdots(i v)$

Adding equations (iii) and (iv), we get

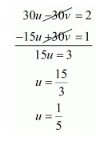
Putting $u=\frac{1}{5}$ in equation (iii), we get

$30 u-30 v=2$

$30 \times \frac{1}{5}-30 v=2$

$6-30 v=2$

$-30 v=2-6$

$-30 v=-4$

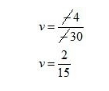
Now, $u=\frac{1}{5}$

$\frac{1}{x}=\frac{1}{5}$

$x=5$

and $v=\frac{2}{15}$

$\frac{1}{y}=\frac{2}{15}$

$y=\frac{15}{2}$

$y=7.5$

Hence, the speed of Ajeet is $5 \mathrm{~km} / \mathrm{hr}$

The speed of Amit is $7.5 \mathrm{~km} / \mathrm{hr}$