Question.
Which of the following pairs of linear equations are consistent/inconsistent? If consistent, obtain the solution graphically :
(i) $x+y=5.2 x+2 y=10$
(ii) $x-y=8,3 x-3 y=16$
(iii) $2 x+y-6=0,4 x-2 y-4=0$
(iv) $2 x-2 y-2=0,4 x-4 y-5=0$
Which of the following pairs of linear equations are consistent/inconsistent? If consistent, obtain the solution graphically :
(i) $x+y=5.2 x+2 y=10$
(ii) $x-y=8,3 x-3 y=16$
(iii) $2 x+y-6=0,4 x-2 y-4=0$
(iv) $2 x-2 y-2=0,4 x-4 y-5=0$
Solution:
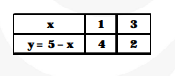
(i) $x+y=5$ ...(i)
$2 x+2 y=10 \quad \ldots$ ...(ii)
$\frac{a_{1}}{a_{2}}=\frac{1}{2}, \frac{b_{1}}{b_{2}}=\frac{1}{2}, \frac{c_{1}}{c_{2}}=\frac{-5}{-10}=\frac{1}{2}$
i.c., $\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}$
Hence, the pair of linear equations is consistent
(i) and (ii) are same equations and hence the graph
is coincident straight line.
(ii) $x-y=8$ ....(i)
$3 x-3 y=16$ ....(ii)
$\frac{a_{1}}{a_{2}}=\frac{1}{3}, \frac{b_{1}}{b_{2}}=\frac{-1}{-3}=\frac{1}{3}, \frac{c_{1}}{c_{2}}=\frac{8}{16}=\frac{1}{2}$
$\Rightarrow \frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{z}}$
Therefore, lines have no solution
Hence, inconsistent
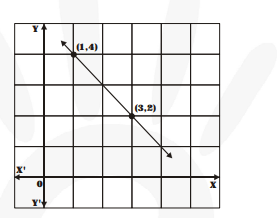
(iii) $2 x+y=6$ ....(i)
$4 x-2 y=4$ ....(ii)
$\frac{a_{1}}{a_{2}}=\frac{2}{4}=\frac{1}{2}, \frac{b_{1}}{b_{2}}=\frac{1}{-2}=\frac{-1}{2}, \frac{c_{1}}{c_{2}}=\frac{6}{4}=\frac{3}{2}$
$\Rightarrow \frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}}$
Therefore, lines have unique solution
Hence, consistent
from (i)
from (ii)
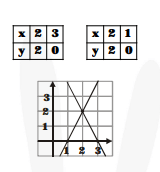
from graph $x=2, y=2$
(iv) $2 x-2 y=2$ ...(i)
$4 x-4 y=5$ ....(ii)
$\frac{a_{1}}{a_{2}}=\frac{2}{4}=\frac{1}{2}, \frac{b_{1}}{b_{2}}=\frac{-2}{-4}=\frac{1}{2}, \frac{c_{1}}{c_{2}}=\frac{2}{5}$
$\Rightarrow \frac{\mathrm{a}_{1}}{\mathrm{a}_{2}}=\frac{\mathrm{b}_{1}}{\mathrm{~b}_{2}} \neq \frac{\mathrm{c}_{1}}{\mathrm{c}_{2}}$
Therefore, lines have no solution.
Hence, Inconsistent.
(i) $x+y=5$ ...(i)
$2 x+2 y=10 \quad \ldots$ ...(ii)
$\frac{a_{1}}{a_{2}}=\frac{1}{2}, \frac{b_{1}}{b_{2}}=\frac{1}{2}, \frac{c_{1}}{c_{2}}=\frac{-5}{-10}=\frac{1}{2}$
i.c., $\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}$

Hence, the pair of linear equations is consistent
(i) and (ii) are same equations and hence the graph
is coincident straight line.

(ii) $x-y=8$ ....(i)
$3 x-3 y=16$ ....(ii)
$\frac{a_{1}}{a_{2}}=\frac{1}{3}, \frac{b_{1}}{b_{2}}=\frac{-1}{-3}=\frac{1}{3}, \frac{c_{1}}{c_{2}}=\frac{8}{16}=\frac{1}{2}$
$\Rightarrow \frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{z}}$
Therefore, lines have no solution
Hence, inconsistent
(iii) $2 x+y=6$ ....(i)
$4 x-2 y=4$ ....(ii)
$\frac{a_{1}}{a_{2}}=\frac{2}{4}=\frac{1}{2}, \frac{b_{1}}{b_{2}}=\frac{1}{-2}=\frac{-1}{2}, \frac{c_{1}}{c_{2}}=\frac{6}{4}=\frac{3}{2}$
$\Rightarrow \frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}}$
Therefore, lines have unique solution
Hence, consistent
from (i)
from (ii)

from graph $x=2, y=2$
(iv) $2 x-2 y=2$ ...(i)
$4 x-4 y=5$ ....(ii)
$\frac{a_{1}}{a_{2}}=\frac{2}{4}=\frac{1}{2}, \frac{b_{1}}{b_{2}}=\frac{-2}{-4}=\frac{1}{2}, \frac{c_{1}}{c_{2}}=\frac{2}{5}$
$\Rightarrow \frac{\mathrm{a}_{1}}{\mathrm{a}_{2}}=\frac{\mathrm{b}_{1}}{\mathrm{~b}_{2}} \neq \frac{\mathrm{c}_{1}}{\mathrm{c}_{2}}$
Therefore, lines have no solution.
Hence, Inconsistent.
