Vijay had some bananas and he divided them into two lots A and B. He sold the first lot at the rate of ₹ 2 for 3 bananas and the second lot at the rate of
₹ 1 per banana and got a total of ₹ 400 If he had sold the first lot at the rate of ₹ 1 per banana and the second lot at the rate of ₹ 4 for 5 bananas, his
total collection would have been ₹ 460. Find the total nmber of bananas he had.
Let the number of bananas in lots A and B be x and y, respectively
Case I Cost of the first lot at the rate of ₹ 2 for 3 bananas + Cost of the second lot at the rate of $₹ 1$ per banana $=$ Amount received
$\Rightarrow \quad \frac{2}{3} x+y=400$
$\Rightarrow \quad 2 x+3 y=1200 \quad \ldots$ (i)
Case II Cost of the first lot at the rate of $₹ 1$ per banana + Cost of the second lot at the rate of ₹ 4 for 5 bananas = Amount received
$\Rightarrow \quad x+\frac{4}{5} y=460$
$\Rightarrow \quad 5 x+4 y=2300 \quad \ldots$ (ii)
On multiplying in Eq. (i) by 4 and Eq. (ii) by 3 and then subtracting them, we get
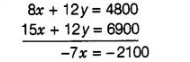
$\Rightarrow \quad x=300$
Now, put the value of $x$ in Eq. (i), we get
$2 \times 300+3 y=1200$
$\Rightarrow \quad 600+3 y=1200$
$\Rightarrow \quad 3 y=1200-600$
$\Rightarrow \quad 3 y=600$
$\Rightarrow \quad y=200$
$\therefore$ Total number of bananas $=$ Number of bana nas in $\operatorname{lot} A+$ Number of bananas in lot $B$
$=x+y$
$=300+200=500$
Hence, he had 500 bananas.
