Verify the division algorithm i.e. Dividend = Divisor × Quotient + Remainder, in each of the following.

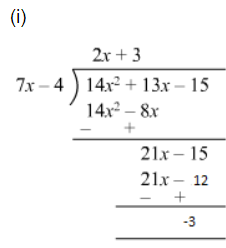
Quotient = 2x + 3

Remainder $=-3$

Divisor $=7 x-4$

Divisor $\times$ Quotient $+$ Remainder $=(7 x-4)(2 x+3)-3$

$=14 x^{2}+21 x-8 x-12-3$

$=14 x^{2}+13 x-15$

$=$ Dividend

Thus,

Divisor $\times$ Quotient $+$ Remainder $=$ Dividend

Hence verified.

(ii)

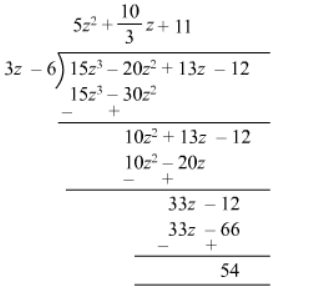
Quotient $=5 z^{2}+\frac{10}{3} z+11$

Remainder $=54$

Divisor $=3 z-6$

Divisor $\times$ Quotient $+$ Remainder $=(3 z-6)\left(5 z^{2}+\frac{10}{3} z+11\right)+54$

$=15 z^{3}+10 z^{2}+33 z-30 z^{2}-20 z-66+54$

$=15 z^{3}-20 z^{2}+13 z-12$

$=$ Dividend

Thus,

Divisor $\times$ Quotient $+$ Remainder $=$ Dividend

Hence verified.

(iii)

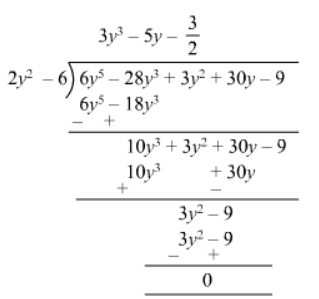
Quotient $=3 y^{3}-5 y+\frac{3}{2}$

Remainder $=0$

Divisor $=2 y^{2}-6$

Divisor $\times$ Quotient + Remainder = $\left(2 y^{2}-6\right)\left(3 y^{3}-5 y+\frac{3}{2}\right)+0$

$=6 y^{5}-10 y^{3}+3 y^{2}-18 y^{3}+30 y-9$

$=6 y^{5}-28 y^{3}+3 y^{2}+30 y-9$

$=$ Dividend

Thus, Divisor $\times$ Quotient + Remainder = Dividend

Hence verified.

(iv)

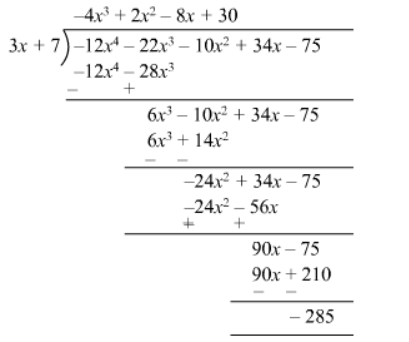
Quotient $=-4 x^{3}+2 x^{2}-8 x+30$

Remainder $=-285$

Divisor $=3 x+7$

Divisor $\times$ Quotient + Remainder $=(3 x+7)\left(-4 x^{3}+2 x^{2}-8 x+30\right)-285$

$=-12 x^{4}+6 x^{3}-24 x^{2}+90 x-28 x^{3}+14 x^{2}-56 x+210-285$

$=-12 x^{4}-22 x^{3}-10 x^{2}+34 x-75$

$=$ Dividend

Thus,

Divisor $\times$ Quotient $+$ Remainder $=$ Dividend

Hence verified.

(v)

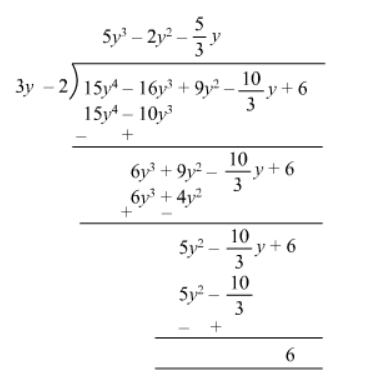
Quotient $=5 y^{3}-2 y^{2}+\frac{5}{3} y$

Remainder $=6$

Divisor $=3 y-2$

Divisor $\times$ Quotient + Remainder $=(3 y-2)\left(5 y^{3}-2 y^{2}+\frac{5}{3} y\right)+6$

$=15 y^{4}-6 y^{3}+5 y^{2}-10 y^{3}+4 y^{2}-\frac{10}{3} y+6$

$=15 y^{4}-16 y^{3}+9 y^{2}-\frac{10}{3} y+6$

$=$ Dividend

Thus,

Divisor $\times$ Quotient $+$ Remainder $=$ Dividend

Hence verified.

(vI)

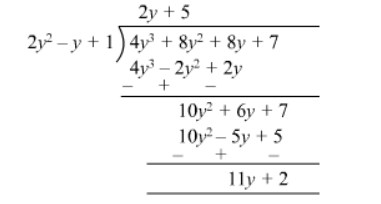
Quotient =  2y + 5

Remainder =  11y + 2

Divisor $=2 y^{2}-y+1$

Divisor $\times$ Quotient $+$ Remainder $=\left(2 y^{2}-y+1\right)(2 y+5)+11 y+2$

$=4 y^{3}+10 y^{2}-2 y^{2}-5 y+2 y+5+11 y+2$

$=4 y^{3}+8 y^{2}+8 y+7$

$=$ Dividend

Thus,

Divisor $\times$ Quotient $+$ Remainder $=$ Dividend

Hence verified.

(vii)

Quotient = 3y2 + 2y + 2

Remainder = 4y2 + 25y + 4

Divisor = 2y3 + 1

Divisor $\times$ Quotient + Remainder $=\left(2 y^{3}+1\right)\left(3 y^{2}+2 y+2\right)+4 y^{2}+25 y+4$

 = 6y5 + 4y4 + 4y3 + 3y2 + 2y + 2 + 4y2 + 25y + 4

  = 6y5 + 4y4 + 4y3 + 7y2 + 27y + 6

= Dividend

Thus,

Divisor $\times$ Quotient $+$ Remainder $=$ Dividend

Hence verified.