Using short cut method, find the mean, variation and standard deviation for the data :

Here, we apply the step deviation method with A = 25 and h = 10

To find: MEAN

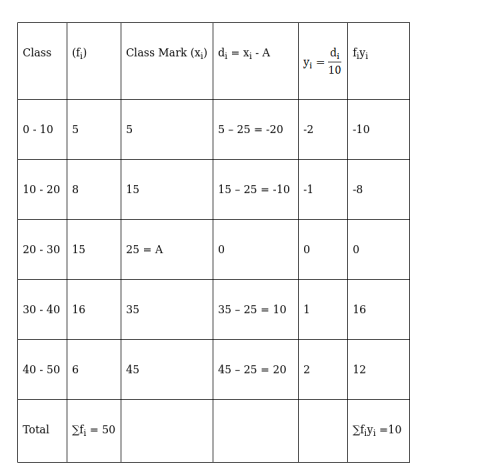
Now, $\quad$ Mean $(\overline{\mathrm{x}})=\mathrm{a}+\mathrm{h}\left(\frac{\sum \mathrm{f}_{\mathrm{i}} \mathrm{y}_{\mathrm{i}}}{\sum \mathrm{f}_{\mathrm{i}}}\right)$

$\Rightarrow \overline{\mathrm{x}}=25+10\left(\frac{10}{50}\right)$

$\Rightarrow \overline{\mathrm{X}}=25+\frac{100}{50}$

$\Rightarrow \overline{\mathrm{x}}=25+2$

$\Rightarrow \overline{\mathrm{x}}=27$

To find: VARIANCE

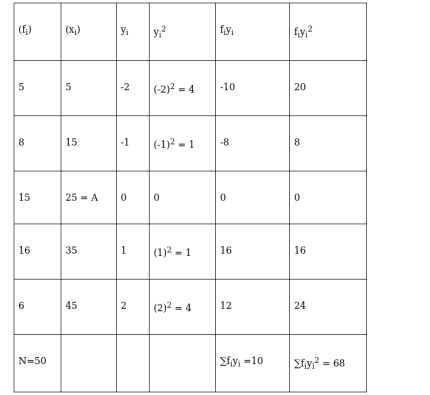
Variance, $\sigma^{2}=\frac{h^{2}}{N^{2}}\left[N \sum f_{i} y_{i}^{2}-\left(\sum f_{i} y_{i}\right)^{2}\right]$

$=\frac{(10)^{2}}{(50)^{2}}\left[50 \times 68-(10)^{2}\right]$

$=\frac{100}{50 \times 50}[3400-100]$

$=\frac{1}{25}[3300]$

$=132$

To find: STANDARD DEVIATION

Standard Deviation $(\sigma)=\sqrt{\text { Variance }}$

$=\sqrt{132}$

$=11.49$