Using short cut method, find the mean, variation and standard deviation for the data

Solution:

To find: MEAN

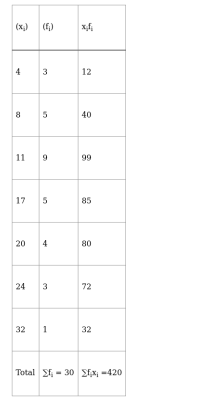
Now,

$\operatorname{Mean}(\overline{\mathrm{x}})=\frac{\sum \mathrm{f}_{\mathrm{i}} \mathrm{x}_{\mathrm{i}}}{\sum \mathrm{f}_{\mathrm{i}}}$

$=\frac{420}{30}$

$=14$

To find: VARIANCE

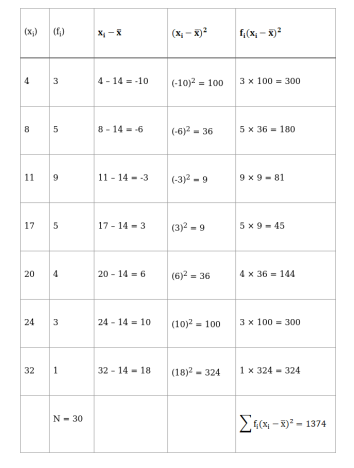
Variance, $\sigma^{2}=\frac{\sum \mathrm{f}_{\mathrm{i}}\left(\mathrm{x}_{\mathrm{i}}-\overline{\mathrm{x}}\right)^{2}}{\mathrm{~N}}$

$=\frac{1374}{30}$

$=45.8$

To find: STANDARD DEVIATION

Standard Deviation $(\sigma)=\sqrt{\text { Variance }}$

$=\sqrt{45.8}$

$=6.77$