Using division of polynomials, state whether

Solution:

(i)

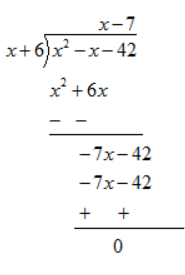
Remainder is zero. Hence (x+6) is a factor of x2 -x-42

(ii)

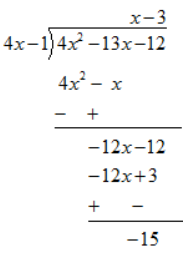
As the remainder is non zero . Hence ( 4x-1) is not a factor of 4x2 -13x-12

(iii)

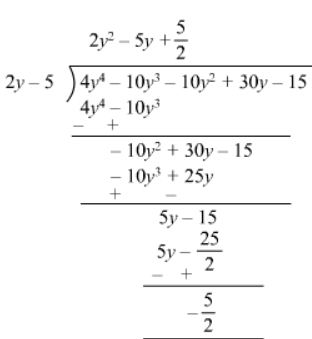
$\because$ The remainder is non zero,

$2 y-5$ is not a factor of $4 y^{4}-10 y^{3}-10 y^{2}+30 y-15$.

(iv)

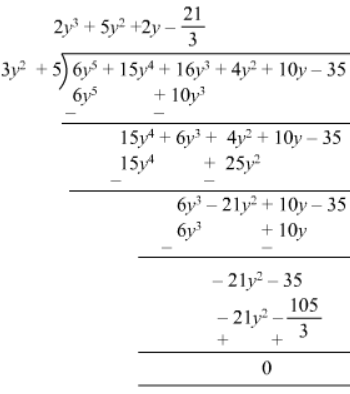
Remainder is zero. Therefore, $3 y^{2}+5$ is a factor of $6 y^{5}+15 y^{4}+16 y^{3}+4 y^{2}+10 y-35$.

(v)

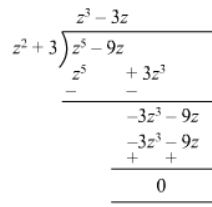
Remainder is zero; therefore, $z^{2}+3$ is a factor of $z^{5}-9 z$.

(vi)

Remainder is zero ; therefore, $2 x^{2}-x+3$ is a factor of $6 x^{5}-x^{4}+4 x^{3}-5 x^{2}-x-15$.