Use Euclid's algorithm to find HCF of 1190 and 1445.
Use Euclid's algorithm to find the HCF of 1190 and 1445. Express the HCF in the form 1190m + 1445n
Using Euclid's division algorithm, we have
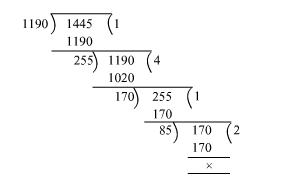
Since 1445 > 1190, we apply Euclid's division lemma to 1445 and 1190 to get;
$1445=1190 \times 1+255$
Since the remainder is not zero, we again apply division lemma to 1190 and 255 and get;
$1190=255 \times 4+170$
Again, the remainder is not zero, so we apply division lemma to 255 and 170 to get;
$255=170 \times 1+85$
Now we finally apply division lemma to 170 and 85 to get;
$170=85 \times 2+0$
Since, in this step, 85 completely divides 170 leaving zero remainder, we stop the procedure.
Hence, the HCF is 85.
Now, using the above division, we have
$170 \times 1+85=255$
$\Rightarrow 85=255-170 \times 1$
$\Rightarrow 85=(1445-1190 \times 1)-(1190-255 \times 4)$
$\Rightarrow 85=(1445-1190)-[1190-(1445-1190) \times 4]$
$\Rightarrow 85=(1445-1190)-[1190-1445 \times 4+1190 \times 4]$
$\Rightarrow 85=1445-1190-[1190 \times 5-1445 \times 4]$
$\Rightarrow 85=1445-1190-1190 \times 5+1445 \times 4$
$\Rightarrow 85=1445 \times 5-1190 \times 6$
Or, $85=1190(-6)+1445(5)$
Hence, $m=-6, n=5$
Common Mistakes Students Make
Understanding where errors creep in is just as important as knowing the correct method.
| Mistake | Why It Happens | How to Avoid It |
|---|---|---|
| Starting with the smaller number (1190) as the dividend | Confusion about which number should be taken as (a) and which as (b) | Always identify the larger number first and use it as the dividend. |
| Stopping too early (e.g., at (r = 170)) | Misreading the stopping condition | Continue the Euclidean Algorithm until the remainder becomes 0. |
| Arithmetic error in Step 2 ((255 \times 4 = 1020), not 1000) | Mental calculation slip | Write out the multiplication explicitly and verify that (1020 + 170 = 1190). |
| Sign error during back-substitution | Not handling negative terms carefully | Use brackets whenever substituting expressions that contain negative terms. |
| Not verifying the final answer | Time pressure or skipping the final check | Substitute the values back into the equation and confirm that (1190 \times (-6) + 1445 \times 5 = 85). |
Frequently Asked Questions
Find answers to common questions.
How do you express HCF in the form 1190m + 1445n?
Work backwards through the division steps (back-substitution). Start from the step that produced the HCF (85 = 255 − 170×1), then substitute expressions for each remainder using earlier steps. After three substitutions, you reach 85 = 1190(−6) + 1445(5). This gives m = −6 and n = 5. Always verify by computing 1190(−6) + 1445(5) = −7140 + 7225 = 85.
What is Euclid's Division Algorithm in simple words?
Euclid's Division Algorithm says: to find the HCF of two numbers, divide the larger by the smaller, note the remainder, then divide the previous divisor by that remainder, and keep repeating until the remainder is zero. The divisor at that final step is the HCF. It is based on the principle that HCF(a, b) = HCF(b, r) where r is the remainder when a is divided by b.
What is the HCF of 1190 and 1445?
The HCF of 1190 and 1445 is 85. This is found by applying Euclid's division algorithm in four steps: dividing 1445 by 1190 (remainder 255), then 1190 by 255 (remainder 170), then 255 by 170 (remainder 85), and finally 170 by 85 (remainder 0). The last non-zero remainder, 85, is the HCF.
What is the difference between HCF and LCM, and how are they related to 1190 and 1445?
HCF (Highest Common Factor) is the largest number that divides both 1190 and 1445 exactly — which is 85. LCM (Lowest Common Multiple) is the smallest number that both 1190 and 1445 divide into. They are related by the formula: HCF × LCM = Product of the two numbers, so LCM = (1190 × 1445) ÷ 85 = 20230. Both concepts are essential for Class 10 boards and competitive exams
. Is Euclid's Division Algorithm in the Class 10 CBSE syllabus?
Yes. Euclid's Division Algorithm is part of Chapter 1 — Real Numbers in the NCERT Class 10 Maths textbook, which is included in the official CBSE Class 10 syllabus. It is also relevant for students studying Number Theory as a foundation topic before JEE. You can find detailed NCERT-aligned solutions at eSaral's NCERT Solutions.
Can m and n be negative in the expression HCF = 1190m + 1445n?
Yes, absolutely. Bézout's Identity guarantees that integers m and n exist, but does not require them to be positive. In this problem, m = −6 is negative and n = 5 is positive. This is the correct and expected answer. Negative values for m or n are common in back-substitution problems and should not be changed.