Question:
Two thin metallic spherical shells of radii $r_{1}$ and $r_{2}$ $\left(r_{1}
Correct Option: 1
Solution:
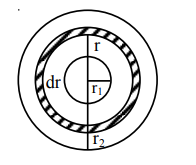
Thermal resistance of spherical sheet of thickness $\mathrm{dr}$ and radius $r$ is
$\mathrm{dR}=\frac{\mathrm{dr}}{\mathrm{K}\left(4 \pi \mathrm{r}^{2}\right)}$
$R=\int_{r_{1}}^{r_{2}} \frac{d r}{K\left(4 \pi r^{2}\right)}$
$\mathrm{R}=\frac{1}{4 \pi \mathrm{K}}\left(\frac{1}{\mathrm{r}_{1}}-\frac{1}{\mathrm{r}_{2}}\right)=\frac{1}{4 \pi \mathrm{K}}\left(\frac{\mathrm{r}_{2}-\mathrm{r}_{1}}{\mathrm{r}_{1} \mathrm{r}_{2}}\right)$
Thermal current (i) $=\frac{\theta_{2}-\theta_{1}}{R}$
$\mathrm{i}=\frac{4 \pi \mathrm{Kr}_{1} \mathrm{r}_{2}}{\mathrm{r}_{2}-\mathrm{r}_{1}}\left(\theta_{2}-\theta_{1}\right)$
