Two tangents making an angle of 120° with each other are drawn

We are given two tangents to a circle making an angle of 120° with each other. The radius of circle is 6 cm

We have to find the length of each tangent.

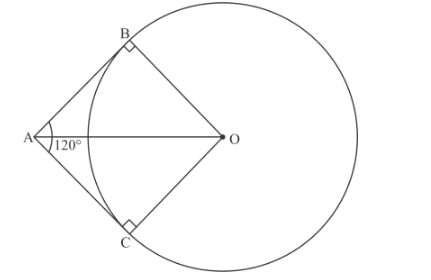
Let O be the center of the given circle

Let AB and AC be the two tangents to the given circle drawn from point A

Therefore 

Now OB and OC represent the radii of the circle

Therefore

 [Since Radius of a circle is perpendicular to tangent]

In $\triangle A B O$ and $\triangle A C O$

$O B=O C$ [Radii of same circle]

$O A=O A \quad[$ Common Side $]$

$A C=A B$ [Tangent segments to a circle from an external point are equal]

Therefore $A B O$ and $\triangle A C O$ are congruent by SSS rule

Hence $\angle B A O=\angle C A O$ [Corresponding angles of congruent triangles]

Now $\angle B A O+\angle C A O=120^{\circ}$

$2 \angle B A O=120^{\circ}$

$\angle B A O=60^{\circ}$

In right $\triangle A B O$

$\frac{O B}{A B}=\tan (\angle B A O)$

$\frac{O A}{A B}=\tan 60^{\circ}$

$\frac{O A}{A B}=\sqrt{3}$

$A B=\frac{O A}{\sqrt{3}}$

$A B=\frac{6}{\sqrt{3}}$

$=\frac{6}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}}$

$=2 \sqrt{3}$

Hence option (d) is correct.