Question:
Two tangents BC and BD are drawn to a circle with centre O, such that ∠CBD = 120°. Prove that OB = 2BC.
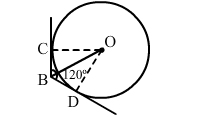
Solution:
Here, $O B$ is the bisector of $\angle C B D$.
( $\mathrm{T}$ wo tangents are equally inclined to the line segment joining the centre to that point)
$\therefore \angle C B O=\angle D B O=\frac{1}{2} \angle C B D=60^{\circ}$
$\therefore$ From $\Delta B O D, \angle B O D=30^{\circ}$
Now, from right - angled $\Delta B O D$,
$\frac{B D}{O B}=\sin 30^{\circ}$
$\Rightarrow \frac{B D}{O B}=\frac{1}{2}$
$\Rightarrow O B=2 B D$
$\Rightarrow O B=2 B C$ (Since tangents from an external point are equal, i. e. $B C=B D$ )
$\therefore O B=2 B C$
