Two satellites $A$ and $B$ of masses $200 \mathrm{~kg}$ and $400 \mathrm{~kg}$ are revolving round the earth at height of $600 \mathrm{~km}$ and $1600 \mathrm{~km}$ respectively. If $\mathrm{T}_{\mathrm{A}}$ and $\mathrm{T}_{\mathrm{B}}$ are the time periods of $\mathrm{A}$ and $\mathrm{B}$ respectively then the value of $T_{B}-T_{A}$ :
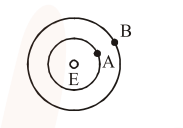
[Given : radius of earth $=6400 \mathrm{~km}$, mass of earth $\left.=6 \times 10^{24} \mathrm{~kg}\right]$
Correct Option: 1
$\mathrm{T}=2 \pi \sqrt{\frac{\mathrm{r}^{3}}{\mathrm{GM}}}$
$\mathrm{T}_{\mathrm{A}}=2 \pi \sqrt{\frac{(6400+600) \times 10^{3}}{\mathrm{GM}}}$
$\mathrm{T}_{\mathrm{A}}=2 \pi \times 10^{9} \sqrt{\frac{7^{3}}{\mathrm{GM}}}$
$\mathrm{T}_{\mathrm{B}}=2 \pi \times 10^{9} \sqrt{\frac{8^{3}}{\mathrm{GM}}}$
$\mathrm{T}_{\mathrm{B}}-\mathrm{T}_{\mathrm{A}}=\frac{2 \pi 10^{9}}{\sqrt{\mathrm{GM}}}[8 \sqrt{8}-7 \sqrt{7}]$
$=314 \times 4.107$
$=1289.64$
$=1.289 \times 10^{3} \mathrm{~s}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.