Two poles of height 6 m and 11 m stand vertically upright on a plane ground.

(b) 13 m

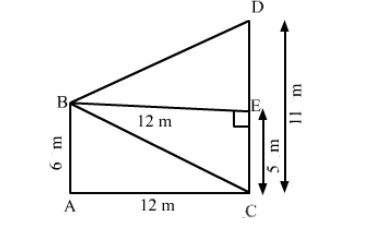
Let the poles be AB and CD.
It is given that:
AB = 6 m and CD = 11 m
Let AC be 12 m.
Draw a perpendicular from B on CD, meeting CD at E.
Then,
BE = 12 m
We have to find BD.
Applying Pythagoras theorem in right-angled triangle BED, we have: ​

$B D^{2}=B E^{2}+E D^{2}$

$=12^{2}+5^{2} \quad(\because E D=C D-C E=11-6)$

$=144+25=169$

$B D=13 \mathrm{~m}$