Two poles of equal heights are standing opposite to each other on either side of the

Let  and  be the two poles of equal height h m.  be the points makes an angle of elevation from the top of poles are 60° and 30° respectively.

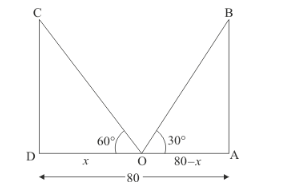
Let $O A=80-x, O D=x .$ And $\angle B O A=30^{\circ}, \angle C O D=60^{\circ}$.

Here we have find height of poles and distance of the points from poles.

We have the corresponding figure as follows.

So we use trigonometric ratios.

In a triangle,

$\Rightarrow \quad \tan 60^{\circ}=\frac{C D}{D O}$

$\Rightarrow \quad \sqrt{3}=\frac{h}{x}$

$\Rightarrow \quad x=\frac{h}{\sqrt{3}}$

Again in a triangle,

$\Rightarrow \quad \tan 30^{\circ}=\frac{A B}{O A}$

$\Rightarrow \quad \frac{1}{\sqrt{3}}=\frac{h}{80-x}$

$\Rightarrow \quad \sqrt{3} h=80-x$

$\Rightarrow \quad \sqrt{3} h=80-\frac{h}{\sqrt{3}}$

$\Rightarrow \sqrt{3} h+\frac{h}{\sqrt{3}}=80$

$\Rightarrow \quad 3 h+h=80 \sqrt{3}$

$\Rightarrow \quad 4 h=80 \sqrt{3}$

$\Rightarrow \quad h=20 \sqrt{3}$

$\Rightarrow \quad x=\frac{20 \sqrt{3}}{\sqrt{3}}$

$\Rightarrow \quad=20$

And

$\Rightarrow \quad O A=80-x$

$\Rightarrow \quad=80-20$

$\Rightarrow \quad=60$

Hence the height of pole is $20 \sqrt{3} \mathrm{~m}$. and distances are $20 \mathrm{~m}, 60 \mathrm{~m}$ respectively.