Question:
Two plane mirrors $M_{1}$ and $M_{2}$ are at right angle to each other shown. A point source ' $P$ ' is placed at ' $a$ ' and ' $2 a^{\prime}$ meter away from $\mathrm{M}_{1}$ and $\mathrm{M}_{2}$ respectively. The shortest distance between the images thus formed is : (Take $\sqrt{5}=2.3$ )
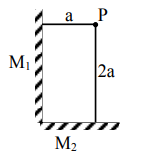
Correct Option: , 2
Solution:
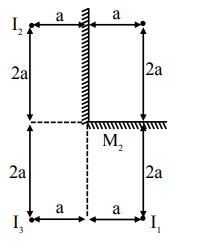
Shortest distance is $2 \mathrm{a}$ between $\mathrm{I}_{1} \& \mathrm{I}_{3}$ But answer given is for $\mathrm{I}_{1} \& \mathrm{I}_{2}$
$\sqrt{(4 a)^{2}+(2 a)^{2}}$
$a \sqrt{20}$
$4.47 \mathrm{a}$
Option (2)
