Two men A and B start with velocities v at the same time

Let’s consider P to be any point at which the two roads are inclined at an angle of 45o.

Now, two men A and B are moving along the roads PA and PB respectively with same speed ‘V’.

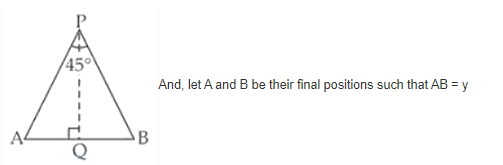
∠APB = 45o and they move with the same speed.

So, ∆APB is an isosceles triangle.

Now, draw PQ ⊥ AB.

We have, AB = y

So, AQ = y/2 and PA = PA = x (assumption)

And, ∠APQ = ∠BPQ = 45o/2 = 22.5o

[As the altitude drawn from the vertex of an isosceles ∆, bisects the base]

Now, in right ∆APQ

sin 22.5o = AQ/AP

$\Rightarrow \sin 22 \frac{1}{2}^{\circ}=\frac{\frac{y}{2}}{x}=\frac{y}{2 x} \Rightarrow y=2 x \cdot \sin 22 \frac{1}{2}^{\circ}$

Differentiating both sides w.r.t, $t$, we get

$\frac{d y}{d t}=2 \cdot \frac{d x}{d t} \cdot \sin 22 \frac{1}{2}^{\circ}$

$\left.=2 \cdot \mathrm{V} \cdot \frac{\sqrt{2-\sqrt{2}}}{2} \quad \because \sin 22 \frac{1}{2}^{\circ}=\frac{\sqrt{2-\sqrt{2}}}{2}\right]$

$=\sqrt{2-\sqrt{2}} \mathrm{~V}$ unit $/ \mathrm{s}$

Therefore, the rate of their separation is

$\sqrt{2-\sqrt{2}} \mathrm{Vm} / \mathrm{s}$