Two lines are respectively perpendicular

Given Two lines m and n are parallel and another two lines p and q are respectively perpendicular to m and n.

i.e.,  p ⊥ m,  p ⊥ n, q ⊥ m, q ⊥ n

To prove p||g

Proof Since, m || n and p is perpendicular to m and n.

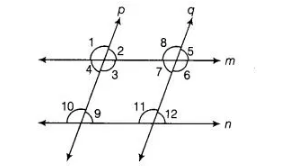
$\therefore$ $\angle 1=\angle 10=90^{\circ}$ [corresponding angles]

Similarly, $\angle 2=\angle 9=90^{\circ}$ [corresponding angles]

$[\because p \perp m$ and $p \perp n]$

$\therefore$$\angle 4=\angle 9=90^{\circ}$ and $\angle 3=\angle 10=90^{\circ}$ [alternate interior angles]

Similarly, if $m \| n$ and $g$ is perpendicular to $m$ and $n$.

Then, $\angle 7=90^{\circ}$ and $\angle 11=90^{\circ}$

Now, $\angle 3+\angle 7=90^{\circ}+90^{\circ}=180^{\circ}$

So, sum of two interior angles is supplementary.

We know that, if a transversal intersects two lines such that a pair of interior angles on the same side of the transversal is supplementary, then the

two lines are parallel.

Hence, p||g.