Two isosceles triangles have equal vertical angles and their areas are in the ratio 36 : 25. Find the ratio of their corresponding heights.
Two isosceles triangles have equal vertical angles and their areas are in the ratio 36 : 25. Find the ratio of their corresponding heights.
Given: Two isosceles triangles have equal vertical angles and their areas are in the ratio of 36:25.
To find: Ratio of their corresponding heights.
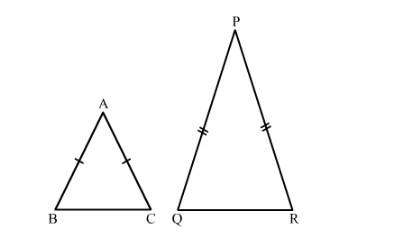
Suppose $\triangle \mathrm{ABC}$ and $\triangle \mathrm{PQR}$ are two isosceles triangles with $\angle \mathrm{A}=\angle \mathrm{P}$.
Now, AB = AC and PQ = PR
$\therefore \mathrm{ABAC}=\mathrm{PQPR}$
In $\triangle \mathrm{ABC}$ and $\triangle \mathrm{PQR}$,
$\angle \mathrm{A}=\angle \mathrm{P}$
$\mathrm{ABAC}=\mathrm{PQPR}$
$\therefore \triangle \mathrm{ABC} \sim \triangle \mathrm{PQR} \quad$ (SAS Similarity)
Let $A D$ and $P S$ be the altitudes of $\triangle A B C$ and $\triangle P Q R$, respectively.
We know that the ratio of areas of two similar triangles is equal to the ratio of squares of their corresponding altitudes.
$\therefore \operatorname{ar} \Delta \mathrm{ABCar} \Delta \mathrm{PQR}=\mathrm{ADPS} 2 \Rightarrow 3625=\mathrm{ADPS} 2 \Rightarrow \mathrm{ADPS}=65$
Hence, the ratio of their corresponding heights is $6: 5$.
