Two heavy spheres each of mass 100 kg and radius 0.10 m are placed 1.0 m apart on a horizontal table.
Two heavy spheres each of mass 100 kg and radius 0.10 m are placed 1.0 m apart on a horizontal table. What is the gravitational force and potential at the mid point of the line joining the centers of the spheres? Is an object placed at that point in equilibrium? If so, is the equilibrium stable or unstable?
0;
$-2.7 \times 10^{-8} \mathrm{~J} / \mathrm{kg}$
Yes;
Unstable
Explanation:
The situation is represented in the given figure:
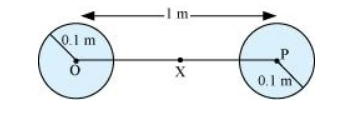
Mass of each sphere, M = 100 kg
Separation between the spheres, r = 1m
X is the mid point between the spheres. Gravitational force at point X will be zero. This is because gravitational force exerted by each sphere will act in opposite directions.
Gravitational potential at point X:
$=\frac{-\mathrm{G} M}{\left(\frac{r}{2}\right)}-\frac{\mathrm{G} M}{\left(\frac{r}{2}\right)}=-4 \frac{\mathrm{G} M}{r}$
$=\frac{4 \times 6.67 \times 10^{-11} \times 100}{1}$
$=-2.67 \times 10^{-8} \mathrm{~J} / \mathrm{kg}$
Any object placed at point X will be in equilibrium state, but the equilibrium is unstable. This is because any change in the position of the object will change the effective force in that direction.
