Two godowns A and B have grain capacity of 100 quintals and 50 quintals respectively. They supply to 3 ration shops, D, E and F whose requirements are 60, 50 and 40 quintals respectively. The cost of transportation per quintal from the godowns to the shops are given in the following table:
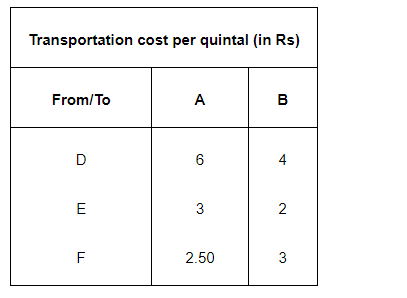
How should the supplies be transported in order that the transportation cost is minimum? What is the minimum cost?
Let godown A supply $x$ and $y$ quintals of grain to the shops $D$ and $E$ respectively. Then, $(100-x-y)$ will be supplied to shop $F$.
The requirement at shop $D$ is 60 quintals since $x$ quintals are transported from godown $A$. Therefore, the remaining $(60-x)$ quintals will be transported from godown $B$.
Similarly, $(50-y)$ quintals and $40-(100-x-y)=(x+y-60)$ quintals will be transported from godown B to shop E and F respectively.
The given problem can be represented diagrammatically as follows.
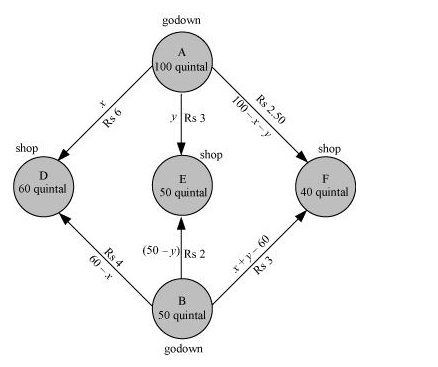
$x \geq 0, y \geq 0$, and $100-x-y \geq 0$
$\Rightarrow x \geq 0, y \geq 0$, and $x+y \leq 100$
$60-x \geq 0,50-y \geq 0$, and $x+y-60 \geq 0$
$\Rightarrow x \leq 60, y \leq 50$, and $x+y \geq 60$
Total transportation cost z is given by,
$z=6 x+3 y+2.5(100-x-y)+4(60-x)+2(50-y)+3(x+y-60)$
$=6 x+3 y+250-2.5 x-2.5 y+240-4 x+100-2 y+3 x+3 y-180$
$=2.5 x+1.5 y+410$
The given problem can be formulated as
Minimize $z=2.5 x+1.5 y+410$ (1)
subject to the constraints,
$x+y \leq 100$ (2)
$x \leq 60$ (3)
$y \leq 50$ (4)
$x+y \geq 60$ (5)
$x, y \geq 0$ (6)
The feasible region determined by the system of constraints is as follows.
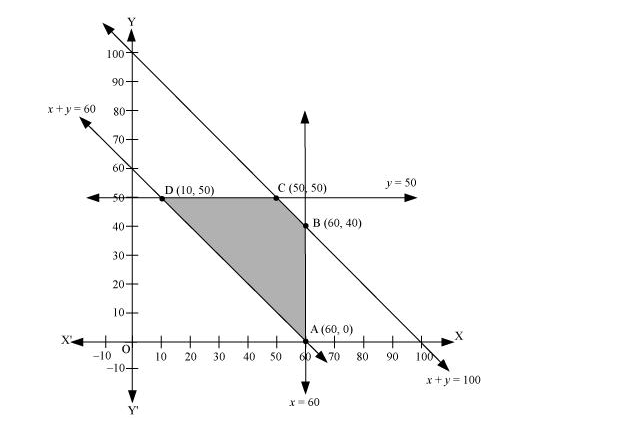
The corner points are A (60, 0), B (60, 40), C (50, 50), and D (10, 50).
The values of z at these corner points are as follows.

The minimum value of z is 510 at (10, 50).
Thus, the amount of grain transported from A to D, E, and F is 10 quintals, 50 quintals, and 40 quintals respectively and from B to D, E, and F is 50 quintals, 0 quintals, and 0 quintals respectively.
The minimum cost is Rs 510.
