Question:
Two equal circles intersect in P and Q. A straight line through P meets the circles in A and B. Prove that QA = QB.

Solution:
Given: Two equal circles intersect at point P and Q.
A straight line passes through P and meets the circle at points A and B.
To prove: QA = QB
Construction: Join PQ.
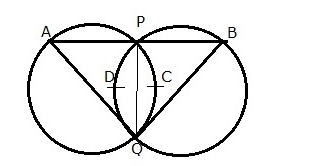
Proof:
Two circles will be congruent if and only if they have equal radii.
Here, PQ is the common chord to both the circles.
Thus, their corresponding arcs are equal (if two chords of a circle are equal, then their corresponding arcs are congruent).
So, arc PCQ = arc PDQ
∴ ∠QAP = ∠QBP (Congruent arcs have the same degree in measure)
Hence, QA = QB (In isosceles triangle, base angles are equal)
