Two equal chords AB and CD of a circle

Given Two equal chords $A B$ and $C D$ of a circle intersecting at a point $P$.

To prove $P B=P D$

Construction Join $O P$, draw $O L \perp A B$ and $O M \perp C D$

Proof We have, $A B=C D$

$\Rightarrow \quad O L=O M$

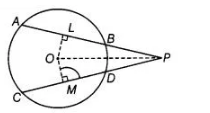
[equal chords are equidistant from the centre]

In $\triangle O L P$ and $\triangle O M P$, $O L=O M$ [proved above]

$\angle O L P=\angle O M P$ [each 90^{\circ] }

$\begin{array}{lll}\text { and } & O P=O P & \text { [common side] }\end{array}$

$\therefore \quad \Delta O L P \equiv \Delta O M P \quad$ [by RHS congruence rule]

$\Rightarrow$ $L P=M P$ $[$ by CPCT $] \ldots(i)$

Now, $A B=C D$

$\Rightarrow$ $\frac{1}{2}(A B)=\frac{1}{2}(C D)$ [dividing both sides by 2]

$\Rightarrow$ $B L=D M$ ....(ii)

[perpendicular drawn from centre to the circle bisects the chord $i . e ., A L=\angle B$ and $C M=M D$ ]

On subtracting Eq. (ii) from Eq. (i), we get

$L P-B L=M P-D M \Rightarrow P B=P D$ 

Hence proved.