Two electrons each are fixed at a distance ' $2 d$ '. A third charge proton placed at the midpoint is displaced slightly by a distance $\mathrm{x}(\mathrm{x}<<\mathrm{d})$ perpendicular to the line joining the two fixed charges. Proton will execute simple harmonic motion having angular frequency : $(\mathrm{m}=$ mass of charged particle)
Correct Option: , 3
From the given condition, we have
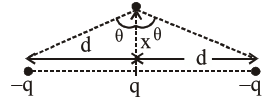
$\mathrm{F}_{\text {netq }}=-\left[2 \mathrm{~F}_{\mathrm{q} / \mathrm{q}} \cos \theta\right]$
$\mathrm{F}_{\text {netq }}=-2 \cdot \frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{\mathrm{q}^{2}}{\left(\sqrt{\mathrm{d}^{2}+\mathrm{x}^{2}}\right)^{2}} \cdot \frac{\mathrm{x}}{\sqrt{\mathrm{d}^{2}+\mathrm{x}^{2}}}$
$=-\frac{\mathrm{q}^{2}}{2 \pi \varepsilon_{0}} \frac{\mathrm{x}}{\left(\mathrm{d}^{2}+\mathrm{x}^{2}\right)^{3 / 2}}$
For $\mathrm{x}<<\mathrm{d}$,
$\mathrm{F}_{\text {net } \mathrm{q}}=-\frac{\mathrm{q}^{2}}{2 \pi \varepsilon_{0} \mathrm{~d}^{3}} \mathrm{x}$
$\therefore \mathrm{a}=-\frac{\mathrm{q}^{2}}{2 \pi \varepsilon_{0} \cdot \mathrm{md}^{3}} \mathrm{x}$
Comparing with equation of SHM $\left(\mathrm{a}=-\omega^{2} \mathrm{x}\right)$
$\therefore \omega=\sqrt{\frac{\mathrm{q}^{2}}{2 \pi \varepsilon_{0} \mathrm{md}^{3}}}$
Hence option (3) is correct
