Two cylindrical vessels are filled with oil.

Solution:

The volume of $1^{\text {st }}$ cylindrical vessel $=\pi \times(15)^{2} \times 20$

$=225 \times 20 \times \pi$

$=4500 \pi \mathrm{cm}^{2}$

The volume of $2^{\text {nd }}$ cylindrical vessel $=\pi \times(12)^{2} \times 16$

$=144 \times 16 \times \pi$

$=1304 \pi \mathrm{cm}^{3}$

Let r be the radius of vessel, which will just contain oil of the both vessels.

Therefore,

Volume of cylindrical vessel = sum of the volume of both vessels.

i.e.,

$\pi r^{2} h=4500 \pi+2304 \pi$

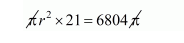
$r^{2}=\frac{6804}{21}$

$r^{2}=324$

$r=18 \mathrm{~cm}$