Two cubes each of volume 27 cm3 are joined end to end to form a solid.

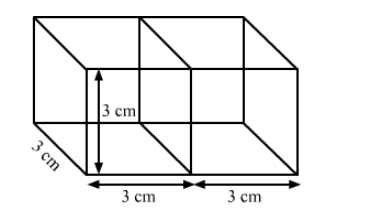
As, volume of a cube $=27 \mathrm{~cm}^{3}$

$\Rightarrow$ (edge) $^{3}=27$

$\Rightarrow$ edge $=\sqrt[3]{27}$

$\Rightarrow$ edge $=3 \mathrm{~cm}$

The length of the resulting cuboid, $l=3+3=6 \mathrm{~cm}$,

its breadth, $b=3 \mathrm{~cm}$ and its height, $h=3 \mathrm{~cm}$

Now, the surface area of the resulting cuboid $=2(l b+b h+h l)$

$=2(6 \times 3+3 \times 3+3 \times 6)$

$=2(18+9+18)$

$=2 \times 45$

$=90 \mathrm{~cm}^{2}$