Two concentric circles are of radii 5 cm and 3 cm, respectively.

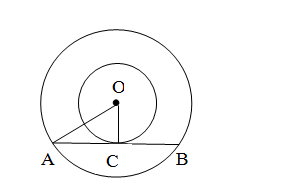
Given: Two circles have the same centre O and AB is a chord of the larger circle touching the
smaller circle at C; also, OA = 5 cm and OC = 3 cm.  

In $\Delta \mathrm{OAC}, \mathrm{OA}^{2}=\mathrm{OC}^{2}+\mathrm{AC}^{2}$

$\therefore \mathrm{AC}^{2}=\mathrm{OA}^{2}-\mathrm{OC}^{2}$

$\Rightarrow \mathrm{AC}^{2}=5^{2}-3^{2}$

$\Rightarrow \mathrm{AC}^{2}=25-9$

$\Rightarrow \mathrm{AC}^{2}=16$

$\Rightarrow \mathrm{AC}=4 \mathrm{~cm}$

$\therefore \mathrm{AB}=2 \mathrm{AC}$ (since perpendicular drawn from the centre of the circle

bisects the chord)

$\therefore \mathrm{AB}=2 \times 4=8 \mathrm{~cm}$

The length of the chord of the larger circle is 8 cm.