Question:
Two circles with equal radii are intersecting at the points $(0$, 1) and $(0,-1)$. The tangent at the point $(0,1)$ to one of the circles passes through the centre of the other circle. Then the distance between the centres of these circles is :
Correct Option: , 2
Solution:
$\because$ Two circles of equal radii intersect each other
orthogonally. Then $R$ is mid point of $P Q$.
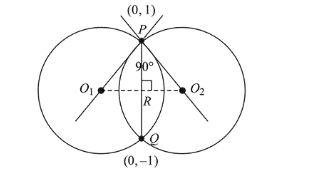
and $P R=O_{1} R=O_{2} R$
$P R=\frac{1}{2} \sqrt{(0-0)^{2}+(1+1)^{2}}=1$
$\therefore$ Distance between centres $=1+1=2$.
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.