Question:
Two circles touch externally at a point P. From a point T on the tangent at P, tangents TQ and TR are drawn to the circles with points of contact Q and R respectively. Prove that TQ = TR.
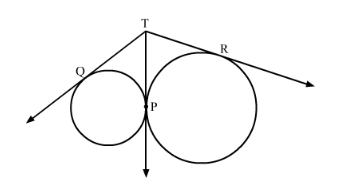
Solution:
We know that the lengths of tangents drawn from an external point to a circle are equal.
In the given figure, TQ and TP are tangents drawn to the same circle from an external point T.
∴ TQ = TP .....(1)
Also, TP and TR are tangents drawn to the same circle from an external point T.
∴ TP = TR .....(2)
From (1) and (2), we get
TQ = TR
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.