Two circles of radii 10 cm and 8 cm intersect each other, and the length of the common chord is 12 cm.

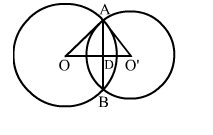
Given: OA = 10 cm, O'A = 8 cm and AB = 12 cm

$A D=\left(\frac{\mathrm{AB}}{2}\right)=\left(\frac{12}{2}\right)=6 \mathrm{~cm}$

Now, in right angled ΔADO, we have:

$O A^{2}=A D^{2}+O D^{2}$

$\Rightarrow O D^{2}=O A^{2}-A D^{2}$

$=10^{2}-6^{2}$

= 100 - 36 = 64

∴ OD = 8 cm

Similarly, in right angled ΔADO', we have:

$O^{\prime} A^{2}=A D^{2}+O^{\prime} D^{2}$

$\Rightarrow O^{\prime} D^{2}=O^{\prime} A^{2}-A D^{2}$

$=8^{2}-6^{2}$

$=64-36$

$=28$

$\Rightarrow O^{\prime} D=\sqrt{28}=2 \sqrt{7} \mathrm{~cm}$

Thus, $O O^{\prime}=\left(O D+O^{\prime} D\right)$

$=(8+2 \sqrt{7}) \mathrm{cm}$

Hence, the distance between their centres is $(8+2 \sqrt{7}) \mathrm{cm}$.