Two chords AB and CD of a circle intersect at a point outside the circle. Prove that

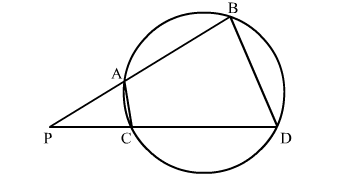
Given: AB and CD are two chords
To Prove:

(a) $\triangle \mathrm{PAC} \sim \triangle \mathrm{PDB}$

(b) PA. PB $=$ PC. PD

Proof:

$\angle \mathrm{ABD}+\angle \mathrm{ACD}=180^{\circ}$    ........(1)

(Opposite angles of a cyclic quadrilateral are supplementary)

$\angle \mathrm{PCA}+\angle \mathrm{ACD}=180^{\circ}$ ...........(2)

   (Linear Pair Angles)

Using (1) and (2), we get

$\angle \mathrm{ABD}=\angle \mathrm{PCA}$

$\angle \mathrm{A}=\angle \mathrm{A} \quad$ (Common)

By AA similarity-criterion $\triangle \mathrm{PAC} \sim \triangle \mathrm{PDB}$

When two triangles are similar, then the ratios of the lengths of their corresponding sides are proportional.

$\therefore \frac{\mathrm{PA}}{\mathrm{PD}}=\frac{\mathrm{PC}}{\mathrm{PB}}$

$\Rightarrow$ PA. PB $=$ PC.PD