Two chords AB and AC of a circle with

False

In figure, AB and AC are two chords of a circle. Join OB and OC.

In ΔOAB and ΔOAC,

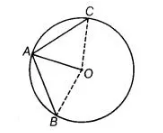
In $\triangle O A B$ and $\triangle O A C_{1}$

$O A=O A$ [common side]

$O B=O C$ [both are the radius of circle]

Here, we are not able to show that either the any angle or third side is equal and $\triangle O A B$ is not congruent to $\triangle O A C$.

$\therefore \quad \angle O A B \neq \angle O A C .$