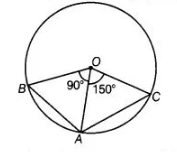
Two chords AB and AC of a circle subtends

In $\triangle B O A$, $O B=O A$ [both are the radius of circle]

$\therefore$ $\angle O A B=\angle O B A$ ...(i)

[angles opposite to equal sides are equal]

$\begin{array}{lll}\ln \triangle O A B, & \angle O B A+\angle O A B+\angle A O B=180^{\circ} & \text { [by angle sum property of a triangle] }\end{array}$

$\Rightarrow \quad \angle O A B+\angle O A B+90^{\circ}=180^{\circ} \quad$ [from Eq. (i)]

$\Rightarrow \quad 2 \angle O A B=180^{\circ}-90^{\circ}$

$\Rightarrow \quad \angle O A B=\frac{90^{\circ}}{2}=45^{\circ}$

Now, in $\triangle A O C$,  $A O=O C$   [both are the radius of a circle]

$\therefore$ $\angle O C A=\angle O A C$ ...(ii)

[angles opposite to equal sides are equal]

Also, $\quad \angle A O C+\angle O A C+\angle O C A=180^{\circ} \quad$ [by angle sum property. of a triangle]

$\Rightarrow \quad 150^{\circ}+2 \angle O A C=180^{\circ} \quad$ [from Eq. (ii)]

$\Rightarrow \quad 2 \angle O A C=180^{\circ}-150^{\circ}$

$\Rightarrow \quad 2 \angle O A C=30^{\circ}$

$\Rightarrow \quad \angle O A C=15^{\circ}$ 

$\angle B A C=\angle O A B+\angle O A C=45^{\circ}+15^{\circ}=60^{\circ}$