Two cars are approaching each other at an equal speed of $7.2 \mathrm{~km} / \mathrm{hr}$. When they see each other, both blow horns having frequency of $676 \mathrm{Hz.}$. The beat frequency heard by each driver will be_____ Hz. [Velocity of sound in air is $340 \mathrm{~m} / \mathrm{s}$.]
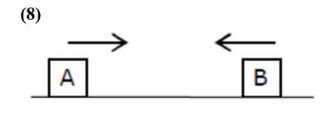
Speed $=7.2 \mathrm{~km} / \mathrm{h}=2 \mathrm{~m} / \mathrm{s}$
Frequency as heard by A $f_{A}^{\prime}=f_{B}\left(\frac{V+V_{0}}{V-V_{n}}\right)$
$f_{A}^{\prime}=676\left(\frac{340+2}{340-2}\right)$
$f_{A}^{\prime}=684 H z$
$\therefore \mathrm{f}_{\text {Beat }}=\mathrm{f}_{\mathrm{A}}^{\prime}-\mathrm{f}_{\mathrm{B}}$
$=684-676$
$=8 \mathrm{~Hz}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.