Two blocks of masses $3 \mathrm{~kg}$ and $5 \mathrm{~kg}$ are connected by a metal wire going over a smooth pulley. The
breaking stress of the metal is $\frac{24}{\pi} \times 10^{2} \mathrm{Nm}^{-2}$.
What is the minimum radius of the wire?
$\left(\right.$ Take $\left.\mathrm{g}=10 \mathrm{~ms}^{-2}\right)$
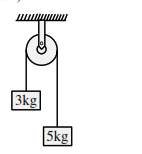
Correct Option: , 3
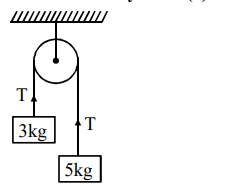
$\mathrm{T}=\frac{2 \mathrm{~m}_{1} \mathrm{~m}_{2} \mathrm{~g}}{\mathrm{~m}_{1}+\mathrm{m}_{2}}=\frac{2 \times 3 \times 5 \times 10}{8}$
$=\frac{75}{2}$
Stress $=\frac{\mathrm{T}}{\mathrm{A}}$
$\frac{24}{\pi} \times 10^{2}=\frac{75}{2 \times \pi R^{2}}$
$\mathrm{R}^{2}=\frac{75}{2 \times 24 \times 100}=\frac{3}{8 \times 24}$
$\Rightarrow \mathrm{R}=0.125 \mathrm{~m}$
$\mathrm{R}=12.5 \mathrm{~cm}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.