Question:
Two blocks $(\mathrm{m}=0.5 \mathrm{~kg}$ and $\mathrm{M}=4.5 \mathrm{~kg})$ are arranged on a horizontal frictionless table as shown in figure. The coefficient of static friction between the two blocks is $\frac{3}{7}$. Then the maximum horizontal force that can be applied on the larger block so that the blocks move together is__________N. (Round off to the Nearest Integer) [Take g as $9.8 \mathrm{~ms}^{-2}$ ]
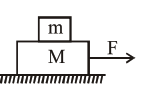
Solution:
$\mathrm{a}_{\max }=\mu \mathrm{g}=\frac{3}{7} \times 9.8$
$\mathrm{F}=(\mathrm{M}+\mathrm{m}) \mathrm{a}_{\max }=5 \mathrm{a}_{\max }$
$=21$ Newton
