Train $A$ and train $B$ are running on parallel tracks in the opposite directions with speeds of $36 \mathrm{~km} /$ hour and $72 \mathrm{~km} /$ hour, respectively. A person is walking in $\operatorname{train} A$ in the direction opposite to its motion with a speed of $1.8 \mathrm{~km} /$ hour. Speed (in $\mathrm{ms}^{-1}$ ) of this person as observed from $\operatorname{train} B$ will be close to : (take the distance between the tracks as negligible)
Correct Option: 1
(1) According to question, train $A$ and $B$ are running on parallel tracks in the opposite direction.
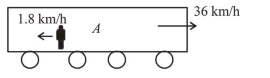
$V_{A}=36 \mathrm{~km} / \mathrm{h}=10 \mathrm{~m} / \mathrm{s}$
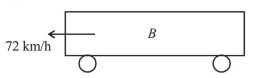
$V_{B}=-72 \mathrm{~km} / \mathrm{h}=-20 \mathrm{~m} / \mathrm{s}$
$V_{M A}=-1.8 \mathrm{~km} / \mathrm{h}=-0.5 \mathrm{~m} / \mathrm{s}$
$V_{\operatorname{man}, B}=V_{\operatorname{man}, A}+V_{A, B}$
$=V_{\operatorname{man}} A+V_{A}-V_{B}=-0.5+10-(-20)$
$=-0.5+30=29.5 \mathrm{~m} / \mathrm{s}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.