To draw a pair f tangents to a circle which are inclined to each other at an angle of 100°, It is required to draw tangents at end points of those two radii of the circle, the angle between which should be:
(a) 100°
(b) 50°
(c) 80°
(d) 200°
Given a pair of tangents to a circle inclined to each other at angle of 100°
We have to find the angle between two radii of circle joining the end points of tangents that is we have to find 
in below figure.
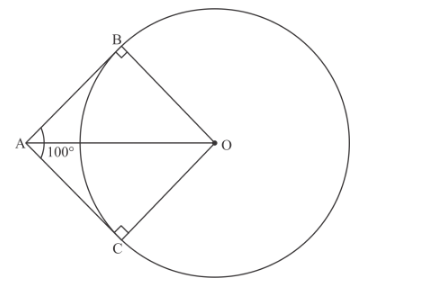
Let O be the center of the given circle
Let AB and AC be the two tangents to the given circle drawn from point A
Therefore ∠BAC = 100°
Now OB and OC represent the radii of the circle
Therefore
[Since Radius of a circle is perpendicular to tangent]
We know that sum of angles of a quadrilateral = 360°
Therefore in Quadrilateral OBAC
$\angle B A C+\angle A C O+\angle C O B+\angle O B A=360^{\circ}$
$100^{\circ}+90^{\circ}+\angle C O B+90^{\circ}=360^{\circ}$
$\angle C O B=360^{\circ}-280^{\circ}$
$\angle C O B=80^{\circ}$
Hence Option (c) is correct.