Question:
To divide a line segment AB in the ratio 5 : 6, draw a ray AY such that ∠BAX is an acute angle, then draw a ray BY parallel to AY and the points A1, A2,
A3,… and B1, B2, B3,… are located to equal distances on ray AY and BY, respectively. Then, the points joined are
(a) A5 and A6
(b) A6 and B5
(c) A4 and B5
(d) A5 and B4
Solution:
(a) Given a line segment AB and we have to divide it in the ratio 5:6.
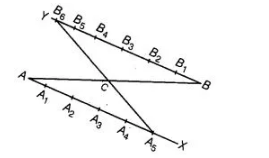
Steps of construction
- Draw a ray AX making an acute ∠BAX.
- Draw a ray BY parallel to AX by making ∠ABY equal to ∠BAX.
- Now, locate the points A1, A 2, A3, A 4 and A5 (m= 5) on AX and B1, B2, B3, B4, B5 and B6 (n = 6) such that all the points are at equal distance from each other.
- Join B6A5. Let it intersect AB at a point C.
Then, AC:BC = 5:6
