Question:
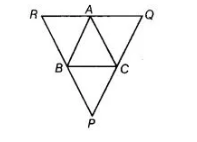
Through A, B and C lines RQ, PR and QP have been drawn, respectively parallel to sides BC, CA and AB of a ΔABC as shown in figure. Show that BC = ½ QR
Solution:
Given In ΔABC, PQ || AB and PR || AC and RQ || BC.
To show BC = ½ QR
Proof In quadrilateral BCAR, BR || CA and BC|| RA
So, quadrilateral, BCAR is a parallelogram.
BC = AR …(i)
Now, in quadrilateral BCQA, BC || AQ
and AB||QC
So, quadrilateral BCQA is a parallelogram,
BC = AQ …(ii)
On adding Eqs. (i) and (ii), we get
2 BC = AR+ AQ
=> 2 BC = RQ
=> BC = ½ QR
Now, BEDF is a quadrilateral, in which ∠BED = ∠BFD = 90°
∠FSE = 360° – (∠FDE + ∠BED + ∠BFD) = 360° – (60° + 90° + 90°)
= 360°-240° =120°
