Three equal circles, each of radius 6 cm,

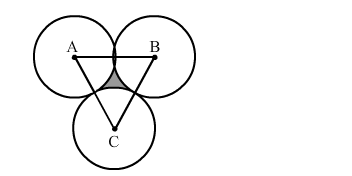
Join ABC. All sides are equal, so it is an equilateral triangle.
Now,

Area of the equilateral triangle $=\frac{\sqrt{3}}{4} \times \operatorname{Side}^{2}$

$=\frac{1.73}{4} \times 12 \times 12$

$=62.28 \mathrm{~cm}^{2}$

Area of the arc of the circle $=\frac{60}{360} \pi \mathrm{r}^{2}$

$=\frac{1}{6} \pi r^{2}$

$=\frac{1}{6} \times \frac{22}{7} \times 6 \times 6$

$=18.86 \mathrm{~cm}^{2}$

Area of the three sectors $=3 \times 18.86=56.57 \mathrm{~cm}^{2}$

Area of the shaded portion = Area of the triangle -">− Area of the three quadrants

$=62.28-56.57$

$=5.71 \mathrm{~cm}^{2}$