Three coins are tossed simultaneously 200 times with the following frequencies of different outcomes
Question.
Three coins are tossed simultaneously 200 times with the following frequencies of different outcomes
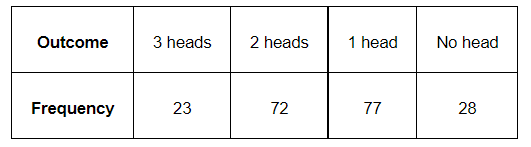
If the three coins are simultaneously tossed again, compute the probability of 2 heads coming up.
Three coins are tossed simultaneously 200 times with the following frequencies of different outcomes
If the three coins are simultaneously tossed again, compute the probability of 2 heads coming up.
Solution:
Number of times 2 heads come up = 72
Total number of times the coins were tossed = 200
$P(2$ heads will come up $)=\frac{\text { Number of times } 2 \text { heads come up }}{\text { Total number of times the coins were tossed }}$
$=\frac{72}{200}=\frac{9}{25}$
Number of times 2 heads come up = 72
Total number of times the coins were tossed = 200
$P(2$ heads will come up $)=\frac{\text { Number of times } 2 \text { heads come up }}{\text { Total number of times the coins were tossed }}$
$=\frac{72}{200}=\frac{9}{25}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.