Three circles of radii a, b, c

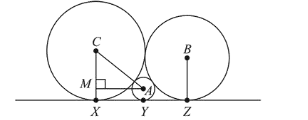
$A M^{2}=A C^{2}-M C^{2}$

$=(a+c)^{2}-(a-c)^{2}=4 a c$

$\Rightarrow A M^{2}=X Y^{2}=4 a c$

$\Rightarrow X Y=2 \sqrt{a c}$

Similarly, $Y Z=2 \sqrt{b a}$ and $X Z=2 \sqrt{b c}$

Then, $X Z=X Y+Y Z$

$\Rightarrow \quad 2 \sqrt{b c}=2 \sqrt{a c}+2 \sqrt{b a}$

$\Rightarrow \quad \frac{1}{\sqrt{a}}=\frac{1}{\sqrt{b}}+\frac{1}{\sqrt{c}}$