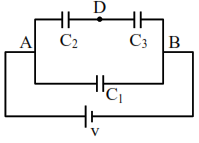
Three capacitors $\mathrm{C}_{1}=2 \mu \mathrm{F}, \mathrm{C}_{2}=6 \mu \mathrm{F}$ and $\mathrm{C}_{3}=12 \mu \mathrm{F}$ are connected as shown in figure. Find the ratio of the charges on capacitors $C_{1}, C_{2}$ and $C_{3}$ respectively :
Correct Option: , 3
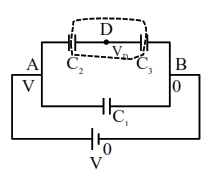
$\left(V_{D}-V\right) C_{2}+\left(V_{D}-0\right) C_{3}=0$
$\left(V_{D}-V\right) 6+\left(V_{D}-0\right) 12=0$
$V_{D}-V+2 V_{D}=0$
$V_{D}=\frac{V}{3}$
$\mathrm{q}_{2}=\left(\mathrm{V}-\mathrm{V}_{\mathrm{D}}\right) \mathrm{C}_{2}=\left(\mathrm{V}-\frac{\mathrm{V}}{3}\right)(6 \mu \mathrm{F})$
$\mathrm{q}_{2}=(4 \mathrm{~V}) \mu \mathrm{F}$
$\mathrm{q}_{3}=\left(\mathrm{V}_{\mathrm{D}}-0\right) \mathrm{C}_{3}=\frac{\mathrm{V}}{3} \times 12 \mu \mathrm{F}=4 \mathrm{~V} \mu \mathrm{F}$
$\mathrm{q}_{1}=(\mathrm{V}-0) \mathrm{C}_{1}=\mathrm{V}(2 \mu \mathrm{F})$
$\mathrm{q}_{1}: \mathrm{q}_{2}: \mathrm{q}_{3}=2: 4: 4$
$\mathrm{q}_{1}: \mathrm{q}_{2}: \mathrm{q}_{3}=1: 2: 2$
